Advanced Lab 5: Odds and ends

This section contains various topics that are of importance but do not necessarily fit the previous narrative.

The psych package contains useful functions especially for psychometric studies. But many of these functions have broader uses. We will provide a brief overview of some functions here, and provide links to the main documentation resources for the package.
ANOVA output can contain different types of results, typically called “type I, II, III” sums of squares. We discuss the differences here.

The psych package

First off, you can access important and helpful documentation about the package in the form of vignettes. You can see all available vignettes, or the vignettes specific to a package, as well as open a specific vignette, using the vignette function provided by R, as the following code demonstrates:

vignette()
vignette(package="psych")           # Three available vignettes
vignette("intro", package="psych")  # Open the "intro" vignette

There is also a lot of information in the accompanying website:

Some of the code uses base R and is different in style than the approach we have taken thus far, but there is plenty of useful information. Here are some functions to check out:

outlier

Computes the so-called Mahalanobis distance of points, to help identify outliers. You must restrict your data to only include scalar variables.

scrub

Can be used to replace parts of the dataset with specific values (e.g. NA). This is an alternative to using the dplyr techniques we have discussed.

error.bars.by

Can produce some basic graphs with error bar information. error.bars is also available.

pairs.panels

Produces a matrix of graphs with information for the various variable interactions. Try pairs.panels(attitude, stars=TRUE) for an example.

corr.test

Computes pairwise correlations and P-values for the associated hypothesis tests. The adjust parameter allows for a number of possible multiple-test adjustments. Try corr.test(attitude) %>% print(short=FALSE) for an example.

This function can be the basis for a function that produces a table with significant correlations flagged. We will show below how to write such a function.

The corrgram package might also be of interest for visualizing correlation matrices.

corPlot

Visually shows the information from corr.test. Try something like:

corPlot(Thurstone, stars=TRUE, numbers=TRUE,
                   upper=FALSE, diag=FALSE)

spider

Shows a spider plot. See also radar. Example:

spider(y=1,x=2:4,data=corr.test(iris[,1:4])$r)

mediate

Provides some tools for mediation analysis.

The psych package also includes a number of datasets that might be useful in demonstrating psychometric topics. See data(package="psych") or the intro vignette for details.

Explicitly flagging significant correlations

We will now see how we can create a function to flag significant correlations in a correlation table. At the same time we will delve into some of the inner workings of R.

We start with the corr.test function in the psych package, and store the result of its call:

cors <- corr.test(iris[,1:4])

We can see the inner structure of this R-object cors by using the str function (or by expanding the cors value in the Environment pane):

str(cors)

This output is a little hard to digest. First of all cors is a “list” of 9 “top-level” items. They each appear following a dollar sign. And in fact we can access them based on the name next to that dollar sign. For example, compare the results of the following two lines with the output from str(cors):

cors$se
cors$adjust

We also see at the very bottom of the str output the line: - attr(*, "class")= chr [1:2] "psych" "corr.test". This tells us that the cors object has a “class” attribute which consists of the two character strings "psych" and "corr.test". Many objects in R have similar outputs; for example the output of a linear model call typically has the class “lm”. The class of an object changes how that object behaves for certain functions, like printing.

Let us take note of a couple more entries in the str(cors) output:

r contains the correlations. It has the “type” num [1:4, 1:4] which means it contains numeric values arranged in a 4 by 4 table. It also has a “dimnames” attribute, which contains the names of the two dimensions of the table.
t contains corresponding t-values. It has the same structure as r.
p contains the corresponding P-values, and it too has the same structure.
ci contains confidence intervals, and it could be used to produce a graphical representation of the information.

As a quick example, let us use the ci information to draw a quick plot of the different correlation confidence intervals.

cors$ci %>%
    rownames_to_column(var="pair") %>%
    ggplot(cis) +
        aes(y=pair, x=r, xmin=lower, xmax=upper) +
        geom_point() +
        geom_text(aes(label=format(r, digits=2)), nudge_y=0.3) +
        geom_errorbarh(height=0.3)

Now let’s see if we can flag the significant correlations:

p <- cors$p
stars <- case_when(
    p < .0001 ~ "****",
    p < .001  ~ "*** ",
    p < .01   ~ "**  ",
    p < .05   ~ "*   ",
    TRUE      ~ "    "
)
dim(stars) <- dim(p)
dimnames(stars) <- dimnames(p)
stars

The dim(...) line sets the dimensions of stars to match those of p, and the dimnames line copies the names for the two dimensions.

This just shows us the star strings separate from the correlations. We now need to merge them together with the correlation values, which are stored in cors$r. First we should format the correlation numbers to a given precision, for printing purposes:

formattedCors <- format(cors$r, digits=2)   # Format the correlations
starredCors <- paste(formattedCors, stars)  # Merge with the stars
dim(starredCors) <- dim(p)
dimnames(starredCors) <- dimnames(p)
as.table(starredCors)

We could manually repeat the above each time, but it might get tedious. A better idea is to create a function that does all these steps for us. When you define a function, you specify a list of parameters for it. When you call the function you need to specify values for the parameters, as we have done many times in these labs. In our case the function will have two parameters:

cors will be the first parameter, and it is expected to be the result of calling corr.test on some dataset.
digits will be the second parameter, specifying how many digits for each correlation we should print. It will default to 2.

Our function returns whatever the last thing is in its body, so we will conclude the function body with the end result we want.

corrFlag <- function(cors, digits=2) {
    p <- cors$p
    stars <- case_when(
        p < .0001 ~ "****",
        p < .001  ~ "*** ",
        p < .01   ~ "**  ",
        p < .05   ~ "*   ",
        TRUE      ~ "    "
    )
    formattedCorrs <- format(cors$r, digits=digits)
    starredCors <- paste(formattedCorrs, stars)
    dim(starredCors) <- dim(p)
    dimnames(starredCors) <- dimnames(p)
    as.table(starredCors)
}
# Example call:
iris[,1:4] %>% corr.test() %>% corrFlag()

An important thing to know about a function is that any names you define within the function will not be added to your environment. So for example the formattedCorrs assignment we make within the function is only meaningful while that function runs, and is forgotten afterwards. We say that these names are local to the function. This helps keep our environment clean.

And here is a different approach: We would like to start with the correlation table, then create a data frame of the pairs of variables and their corresponding correlations. Then we can add a column that has the star information. Let’s take a look. We’ll perform the following steps:

First we use as.data.frame to turn the cors$r array into a data frame.
Then we use rownames_to_column to bring in the row names as a new column.
Lastly, we gather the remaining columns into one.

corrsDf <- cors$r %>% as.data.frame() %>%
            rownames_to_column(var="var1") %>%
            gather(key="var2", value="r", -var1)
corrsDf

Now we do the same thing for the t and p values:

corrsTs <- cors$t %>% as.data.frame() %>%
            rownames_to_column(var="var1") %>%
            gather(key="var2", value="t", -var1)
corrsPs <- cors$p %>% as.data.frame() %>%
            rownames_to_column(var="var1") %>%
            gather(key="var2", value="p", -var1)

Now we use inner_join to bring these three frames together:

df <- corrsDf %>% inner_join(corrsTs) %>% inner_join(corrsPs)

Now we want to restrict df to only consider each pair of variables once, and to never pair a variable with itself. As our rows came from the table, many entries are duplicated right now. We can simply compare the variable names for this, and only keep the instances where the first name is alphabetically previous to the second name. We then arrange the rows by the p-values:

df %>%
    filter(var1 < var2) %>%
    arrange(p)

We can now add a star column to this data frame. Instead of using case_when as above, we will use cut to end up with an ordered factor. Finally, we will use unite, the opposite of separate, to bring the two variable names together into a pair:

finalDf <- df %>%
    filter(var1 < var2) %>%
    arrange(p) %>%
    mutate(sig=cut(p, breaks=c(0, .0001, .001, 0.01, 0.05, 1),
                      labels=c("****", "*** ", "**  ", "*   ", "    "),
                      include.lowest=TRUE)) %>%
    unite(col="pair", var1, var2, sep="-", remove=TRUE)
finalDf

We could of course turn this into a function for more general use (homework!).

ANOVA output types

When considering the output of an ANOVA analysis, there are different kinds of “sum of squares” computations and tests that we can be performing. They all come down to which models we are trying to compare. As a running example, let us consider a small dataset that is used in the SAS documentation:

data<-tribble(
    ~Family, ~Gender, ~Height,
    1,"F",67,
    1,"F",66,
    1,"F",64,
    1,"M",71,
    1,"M",72,
    2,"F",63,
    2,"F",63,
    2,"F",67,
    2,"M",69,
    2,"M",68,
    2,"M",70,
    3,"F",63,
    3,"M",64,
    4,"F",67,
    4,"F",66,
    4,"M",67,
    4,"M",67,
    4,"M",69
)
data <- data %>% mutate(Family=factor(Family), Gender=factor(Gender))
data %>% count(Family, Gender)

So we have here two factors, namely Family and Gender, and a scalar response Height.

We can see that this is an unbalanced design, with unequal cell sizes. A consequence of this lack of balance is that contrast-coded variables will be correlated. This results in a number of different SS computations and disagreements about which one to use. Good resources for this discussion are the following:

Working with unbalanced cell sizes in multiple regression with categorical predictors by Ista Zahn
Anova – Type I/II/III SS explained
A critique of some of the approaches, by Bill Venables.

The differences arise from the kind of hypothesis we want to test. We can roughly consider the following graphical depiction of the various models we have in our example:

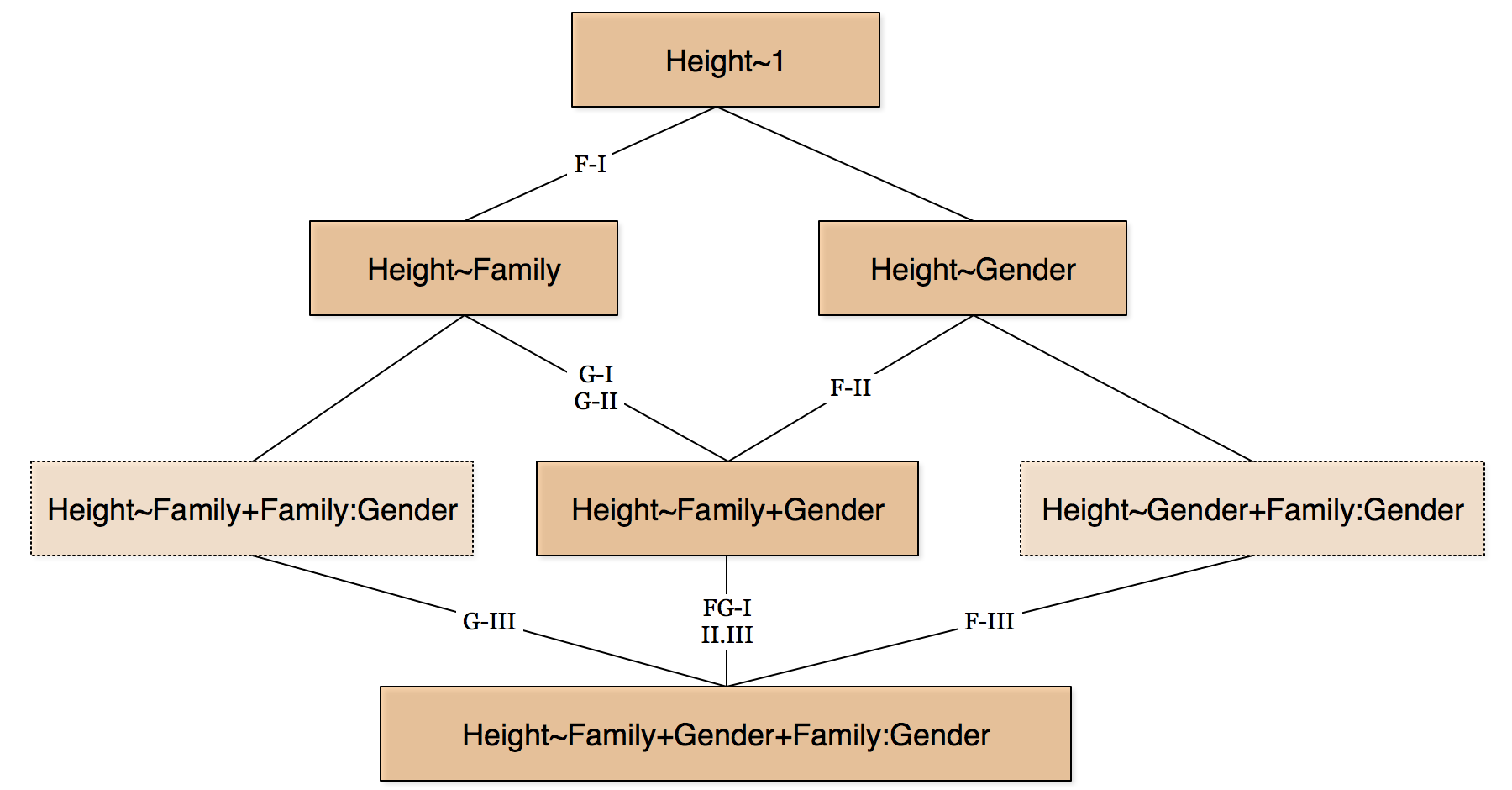
The classification into three different types comes from SPSS and SAS and has become common practice. Briefly:

Type I: Factors are compared sequentially as they are being added to the model. So if the model is Height~Family+Gender+Family:Gender, then we first consider the effect of Family compared to the null model, then we consider the effect of Gender in the presence of Family, and finally we consider the effect of the interaction term in the presence of both Family and Gender.
Type II: Factors are considered against a model that contains all the other factors, but assuming no interactions. This tends to only be meaningful in the absence of interactions.
Type III: We consider factors against a model that contains all the other factors including all the interactions. In order for the calculations to work correctly, it is of vital importance that zero-sum coding constrasts be used for the factor variables. This is not the default in R so you must set the contrasts correctly first before starting your model work, if you want to use Type III sums of squares.

Some things to keep in mind:

SAS produces type III and type II SSs by default in its ANOVA procedure.
R produces type I SSs by default in its anova method.
The car package which you can install provides an Anova method (capital A), which has a type option. So you can something like: Anova(fit1, type="III") to get type III SSs.
However, for this to return the correct SSs, you also need to have specified the correct contrasts in the fit. The simplest way to do that is to set up the global options for contrasts. The command needed for that is options(contrasts=c("contr.sum", "contr.sum")). You must set that before you do the model fit. Some would argue that the reliance on a specific type of contrast (which should in theory have no effect on the final conclusions) is a considerable weakness of the type III SSs. It is a bit analogous to our results suddenly changing because we rescaled our values to have a different mean and standard deviation.
It is better to instead think of the question in terms of the models depicted in the picture above, and the comparisons between them. In fact, you can carry those comparisons directly instead via calls like this: anova(fit1, fit2).
Different SS Types tend to answer different hypotheses. So it is important to consider what hypothesis you are trying to test first.
Some people would object to the consideration of a model like Height~Family+Family:Gender in the first place, arguing that if you add an interaction term in a model then you must also add the “lower”/“marginal” terms, i.e. Family and Gender. Hence some people would object to considering the two differently-colored models at all, and would argue that considering the type III SSs is somewhat meaningless: In the presence of a significant interaction effect, it is pointless to assess/test the significance of its marginal effects, as they should always be included.
On balanced designs all three types produce the same results (even though they conceptually test different hypotheses).

This last point deserves further discussion that the available time would permit.